This page is a personal scratchpad.

#Coinage
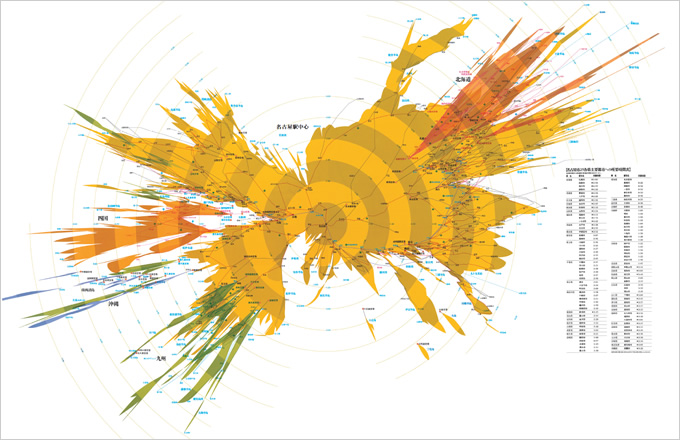
杉浦康平 - 時間地図

よさの探索空間において、ある位置から別の位置までの移動を、そのインターフェースを用いて何手の操作で完了できるかを表す概念。幾何学的に厳密な意味での距離ではなく、移動時間や歩数のようなものと考えてください。

マンハッタン距離

たとえば、ポケモンやボンバーマンのようなゲームで、十字キーをつかって主人公を動かす場合について考えてみます。たとえば、すぐ上のマスに移動するには↑の1手の入力で済みますが、斜め右上のマスの場合、↑ → の2手が必要、といった具合です。

2点$$ p $$、$$ q $$ 間の操作距離はこのようになります。

$$ D(p, q) = |p_ - q_| + |p_ - q_| $$

水平方向の距離と垂直方向の距離の和です。碁盤の目の道路上の道のりに似ていることから、マンハッタン距離と呼ばれます。
中心を現在位置、マス内の数字を操作距離とすると、こんな感じに図式化できます。

ユークリッド距離

仮に、十字キーの代わりにアナログスティックが使えた場合、その操作距離は普段私たちが考える直線距離になります。これはユークリッド距離とも呼ばれます。

$$ D(p, q) = \sqrt{(p_x - q_x)^2 + (p_y - q_y)^2} $$

図式化するとこんな感じ。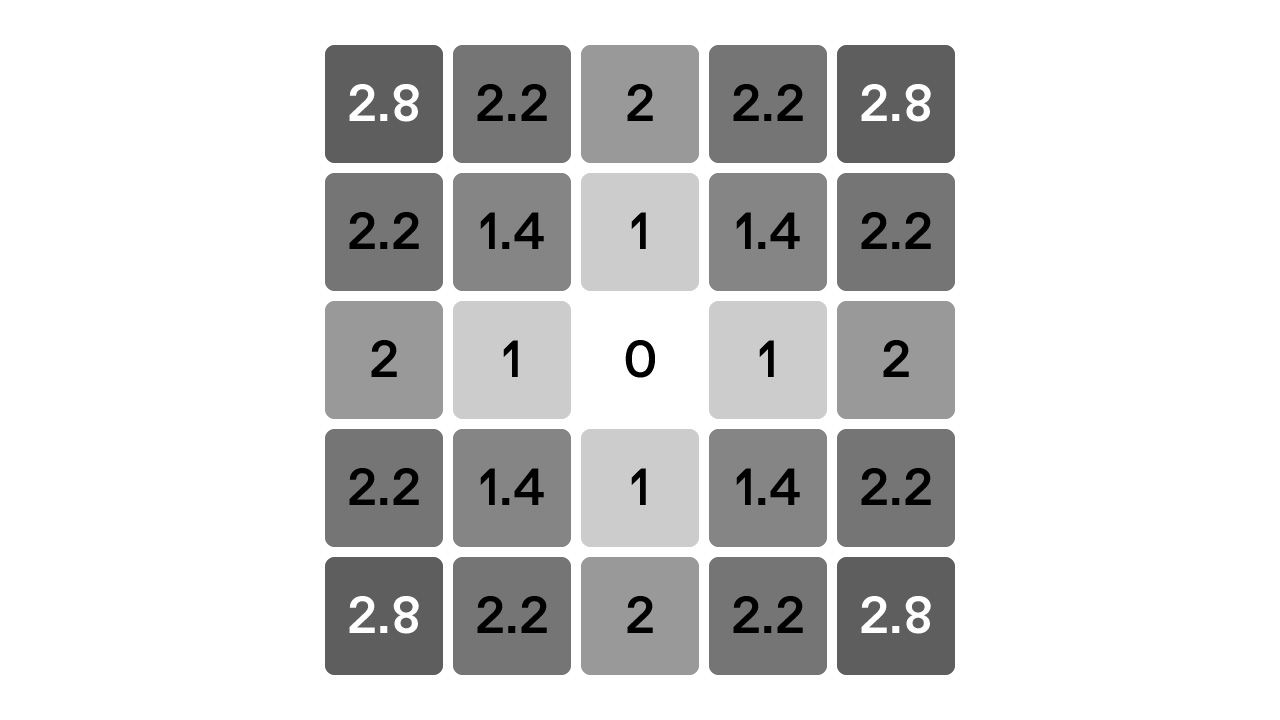

その他の操作距離

では、テンキーでX座標とY座標とをフォームに数値入力できる場合はどうでしょうか。ゲームとしては遊びづらいことこの上ないですが。移動先の座標は頭に入っているものとします。数値入力を桁の大きさなどを問わず1手とカウントした場合、このようになります。

$$ D(p, q) = \left{\begin{array}{ll}0 & \text{if}\ \ p = q \1 &\text{if}\ \ p_x = q_x\ \ \text{or}\ \ p_y = q_y\2 & \text{otherwise.}\end{array}\right. $$

ルークや飛車が任意の位置に移動するのに何手かかるか? を表したものと考えると分かりやすいです。（baku89.iconは勝手に「飛車距離」と呼んでいます）

このように、インターフェースの性質は操作距離を規定します。ちなみに、冒頭画像の杉浦康平の『時間地図』は、交通機関を用いた移動を「操作距離」とみなした時の正距方位図といえます。

メモ

• 同時に1つずつしか調整することのできない1次元の入力の集まりからなるインターフェースの操作距離はマンハッタン距離
  • 十字キー
  • スライダーからなるミキサー卓（ただし、多くのレコーディング・エンジニアは両手の指を同時に操る）
• 入力の並列化は操作距離をユークリッド距離にする
  • 2ハンドル型水栓 = マンハッタン距離、レバー型混合水栓 = ユークリッド距離
  • Etch A Sketch = マンハッタン距離、スタイラス = ユークリッド距離
• 「操作にかかる平均時間」という連続量についても定式化したい
  • 入力のぶれや、（そのツマミに触れる、触れ終えるのにかかる）予備・予後動作の時間、方向転換のコストを加味する
  • フィッツの法則は、操作距離がユークリッド距離のポインティングデバイスについての定式化
  • ある次元に着目したとき、ある値を別の値に変更するのにかかる時間でインターフェースを分類する
    • 定数時間：値の直接入力、ドロップダウン（あまり数が多くない場合）
      • ⭕ 値の表記が具体的に分かっており、どの値も現在値によらず一様に現れる可能性のあるパラメーター
        • 例）誕生日、文字
    • 線形時間
      • カウント方式： 方向キー、数値入力の横の上下矢印
        • ⭕ グリッド上の位置合わせなど、望ましい値が離散的なパラメーター
      • 速度入力方式：ジョイスティック、ThinkPadの赤ポッチ
        • ⭕ 細かい位置合わせを必要とせず、操作の運動量を値の変化量に依らず最小に留めたいとき
    • 対数時間：ポインティングデバイス、スライダー、ロータリーノブ
      • ⭕ 広い範囲を取り得る連続量
      • ただし、身体のブレを最も拾いやすいので、ファインチューニングが必要なパラメーターは入力スケールを変更できる必要がある
        • 液タブで絵を書く時、拡大縮小は必須機能
        • ミキサー卓のロータリーノブやスライダーのスケールは物理的に変えることができないが、精度をそこまで必要としないので必要十分
          • つまみの位置から絶対位置が分かり、絶妙なツマミの上下で相対的な変化を与えられるので良い